Objectifs : - Prise en main du logiciel Déclic32 à travers un exemple
- Apport de connaissances mathématiques : droite et cercle d'Euler.
1. Constructions géométriques lancer Déclic32 : Démarrer/Programmes/Maths/Déclic32
1.1. Tracé du triangle ABC A l'aide de la souris, construire un triangle de sommets A, B et C.
Utiliser toute la surface de l'écran.
Par les menus | Par la barre d'outils | Menu Construire/Triangles/triangles 3 points |  |
| Nommer les sommets en les sélectionnant par un clic avec le bouton droite puis gauche de la souris pour faire apparaître la boite de dialogue ci-contre. Cette boite de dialogue permet de renseigner le nom de l'objet créé, sa couleur, le style et l'épaisseur du trait. | 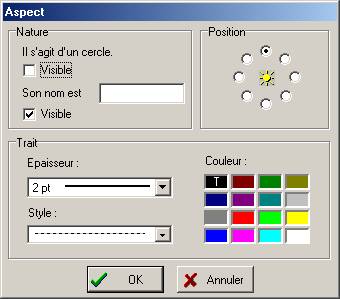
|
| Une autre solution consiste à utiliser la boite de dialogue ci-contre | 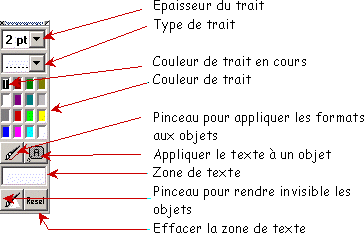 |
1.2. Tracés des médiatrices Tracer les médiatrices des trois côtés du triangle ( En vert et en trait plein)
Par les menus | Par la barre d'outils | Menu Construire/Médiatrice |  |
Le logiciel demande simplement de cliquer le segment adéquat. Voir l'aide dans la barre d'information en bas de l'écran.
1.3. Construction des milieux. Construire les milieux des 3 côtés du triangle ABC. ces points n'existent pas encore, il faut les créer. (C'est ce qui diffère de la géométrie au tableau !)
Par les menus | Par la barre d'outils | Menu Construire/Milieu |  |
On appelle A' le milieu de [BC], B' le milieu de [AC] et C' le milieu de [AB].
1.4. Tracé du cercle C circonscrit au triangle ABC. Rappel : le centre du cercle circonscrit est l'intersection des médiatrices. Création du point d'intersection Ce point n'existe pas encore, il faut le créer. (C'est ce qui diffère de la géométrie au tableau !)
Par les menus | Par la barre d'outils | Menu Construire/Intersection |  |
Il suffit de cliquer sur 2 des 3 médiatrices. Soit O ce point. Création du cercle :
Par les menus | Par la barre d'outils | Menu Créer/Cercle 2 points |  |
Cliquer le centre puis un point du cercle. Déclic32 trace le cercle avec la dernière couleur utilisée ; pour le dessiner en vert, cliquer le cercle avec le bouton droit de la souris et choisir le vert Nommer le cercle C.
1.5. Tracé des 3 médianes a) Tracer les 3 médianes AA', BB' et CC' ( En rouge et grands pointillés)
Par les menus | Par la barre d'outils | Menu Créer/Droite 2 points |  |
b) Construction du centre de gravité du triangle ABC Soit G le centre de gravité ( Intersection des médianes)
Par les menus | Par la barre d'outils | Menu Construire/Intersection |  |
c) Construction des 3 hauteurs AA1, BB1 et CC1 du triangle ABC ( En bleu et grands pointillés)
Par les menus | Par la barre d'outils | Menu Construire/Perpendiculaire |  |
d) Construction de l'orthocentre H du triangle ABC (Intersection des hauteurs)
Par les menus | Par la barre d'outils | Menu Construire/Intersection |  |
1.6. Pour plus de lisibilité, on va rendre les objets suivants transparents :
- Le cercle C
- les médiatrices
- Les médianes
- Les hauteurs
Pour cela, sélectionner l'objet en le cliquant avec le bouton droit de la souris, deux fois si nécessaire et décocher la case visible. |  |
2. La droite d'EULER Tracer en bleu et en gras le segment OH.
Par les menus | Par la barre d'outils | Menu Créer/Segment 2 points |  |
Passe-t-il par G ?.............. Comment sont les points O, H et G ?...................... Vérifier que cette propriété reste vraie quelque soit le triangle ABC. En cliquant sur le point A, par exemple, avec le bouton gauche de la souris, faire bouger ce point et observer.
La droite (OH) est appelée la droite d'EULER du triangle ABC. |
Mesurer OG et GH (Il faut auparavant les créer)
Par les menus | Par la barre d'outils | Menu Décrire/Mesurer |  |
Cliquer sur le segment OG, recommencer la manipulation avec le segment GH. OG = ................. GH = ...............
Calculer les rapports 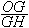 et et 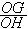 : :
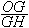 =............... =............... 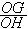 =............... =............... Recommencer ces calculs en modifiant la position du point A 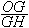 =............... =...............  =............... =...............
| Compléter : OG = ..........GH et OG = ................OH |
3. Le cercle d'EULER En procédant de la même façon que précédemment, réaliser les constructions géométriques demandées ci-dessous. a) Soit O' le milieu du segment OH Construire le cercle C' en rouge de centre O' passant par les points A', B' et C'(Cercle 2 points). Par quels autres points passe-t-il ?
Ce cercle s'appelle " le cercle des 9 points d'EULER du triangle ABC" |
b) Détermination des 3 autres points. Soient A2, B2 et C2 les points d'intersection des hauteurs avec le cercle C.| Mesurer : AA2 = .......... BB2 = .......... CC2 = .......... A2H = .......... B2H = .......... C2H = .......... |
Que peut-on constater ? A2 est .....................................du segment.......................
B2 est .....................................du segment.......................
C2 est .....................................du segment....................... |
c) Conclusion : Le cercle d'EULER du triangle ABC contient. les ................................................................. les ................................................................. les .................................................................
|
4. Exemple de copie d'écran 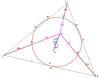
Télécharger le fichier Word zippé : 
|